Daten richtig interpretieren: Hypothesentests im Google Ads Konto

Bei der Optimierung von Google Ads Kampagnen können für viele Merkmale Gebotsanpassungen vorgenommen werden: Für Geräte, Tage und Uhrzeiten und sogar spezifische demographische Merkmale wie Geschlecht, Altersgruppen und Einkommen.

Insbesondere wenn zu wenig Conversion-Daten für Smart-Bidding Gebotsstrategien zur Verfügung stehen, müssen die Gebote manuell angepasst und optimiert werden. 

Vergleicht man die Werte eines Merkmals untereinander, ergeben sich sehr oft gravierende Unterschiede in der Performance. Auch wenn in vielen Fällen eine Gebotsanpassung verlockend erscheint, ist diese oft nicht sinnvoll oder sogar kontraproduktiv, da der Zufall eine große Rolle spielt. 

Wie Sie Muster und Zufall Ihrer Daten auseinanderhalten

Aber was ist Zufall, was Muster? Hier können statistische Signifikanztests oder Hypothesentests eine Antwort geben.

Vergleicht man beispielsweise die Conversion-Rate zwischen Männern und Frauen, fallen in den meisten Konten schnell Unterschiede auf:

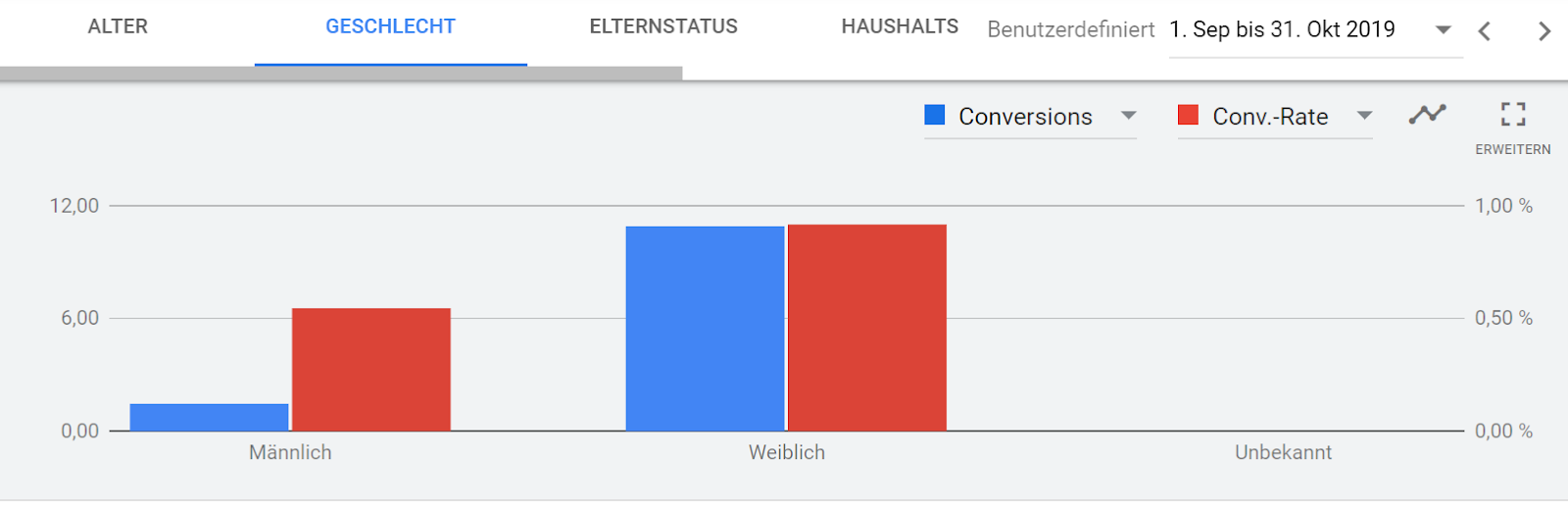
Abb. 1: Vergleich Conversion Rate Männer/Frauen

Die obere Grafik scheint zu verdeutlichen, dass Männer in diesem Fall erstens deutlich weniger kaufen und zweitens eine deutliche geringere Conversion-Rate haben.

Hierfür eine Erklärung zu finden ist oft nicht schwer – insbesondere wenn man sich an gängigen Klischees bedient: Männer shoppen nun einmal nicht so gern wie Frauen und kaufen weniger ein.

Sähe die Grafik andersherum aus, könnte man argumentieren, dass Frauen nun einmal wählerischer sind und lieber im Laden kaufen. Die Wahrheit ist jedoch häufig, dass es sich um reinen Zufall handelt. 

Der Erwartungswert

Um ein erstes Gefühl dafür zu geben, welche Faktoren hier eine Rolle spielen, ein kurzer Ausflug in die Theorie: Notiert man bei einem Münzwurf für jedes Mal Kopf eine 0 und jedes Mal Zahl eine 1, hat jeder Wurf einen Erwartungswert von 0,5:

0,5 * 0 + 0,5 * 1 = 0,5 

(Wahrscheinlichkeit für Ereignis A) * (Ereignis A) + (Wahrscheinlichkeit für Ereignis B) * (Ereignis B) = Erwartungswert

Wirft man die Münze ein einziges Mal, notiert man entweder 0 oder 1. Die Differenz zum Erwartungswert ist demnach in jedem Fall 0,5. Wirft man die Münze zweimal, notiert man eines von vier möglichen Ergebnissen: 0-0, 0-1, 1-0, 1-1. Die Differenz zum Erwartungswert beträgt entweder 0,5 oder 0.

Die weiteren Schritte seien vorweggenommen: Je öfter man die Münze wirft, desto näher wird der beobachtete Wert am Erwartungswert liegen. Die folgenden Grafiken verdeutlichen die relative Häufigkeit der möglichen Differenzen zum Erwartungswert jeweils für unterschiedliche Datenmengen:

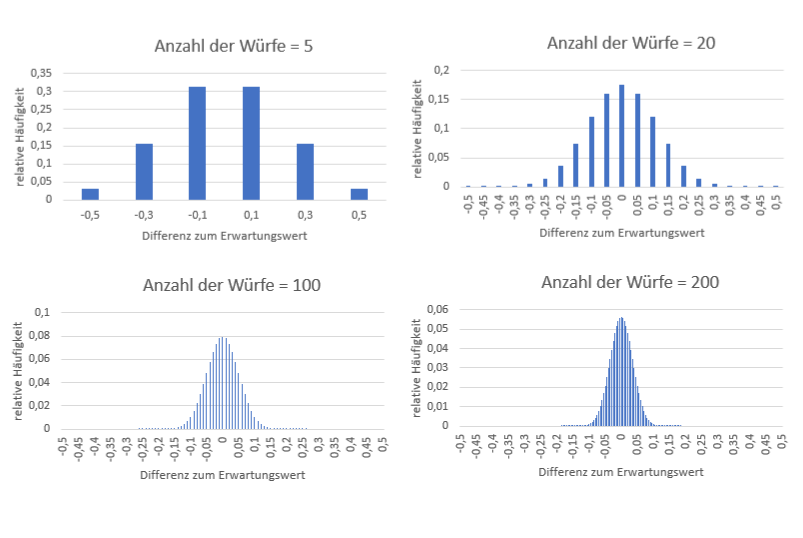
Abb. 2: Verschiedene Erwartungswerte in Abhängigkeit der Würfe

Diesen Grenzwertsatz bezeichnet man in der Stochastik als Gesetz der großen Zahl: Je größer die Stichprobe, desto größer die Wahrscheinlichkeit, dass der beobachtete Wert sehr nah an der tatsächlichen Wahrscheinlichkeit liegt. Im Umkehrschluss bedeutet dies automatisch, dass starke Abweichungen zum Erwartungswert wahrscheinlicher werden, je kleiner die gewählte Stichprobe ist. 

Zurück zum obigen Beispiel der Conversion-Raten für Frauen und Männer im Ads Konto: Schaut man auf die Achsen fällt auf, das trotz eines Zeitraums von 2 Monaten verhältnismäßig wenig Daten vorhanden sind – es handelt sich also um einen kleinen Account.

Hier ist also äußerste Vorsicht geboten.

Das Erkennen eines Musters wird außerdem umso schwieriger, je mehr Merkmale vorhanden sind: Während bei der Betrachtung des Geschlechts nur die drei Ausprägungen Weiblich, Männlich und Unbekannt in Frage kommen, gibt es bei der Analyse der verschiedenen Altersgruppen insgesamt 7 Kategorien:

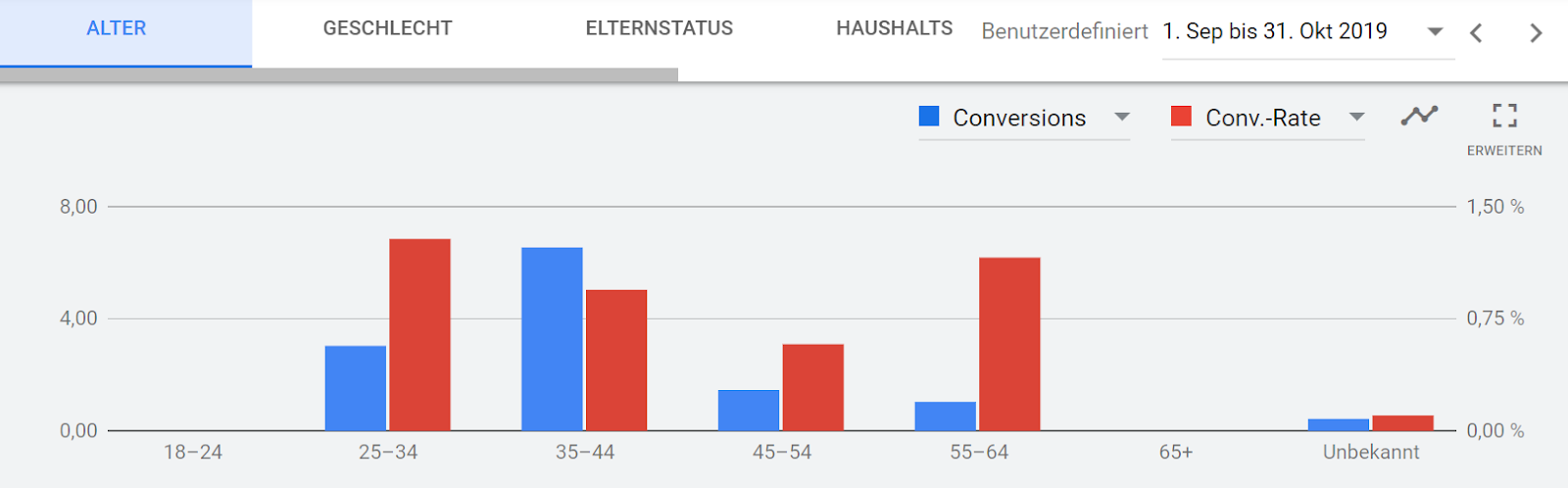
Abb. 3: Weitere Merkmale im Vergleich: Alter und Geschlecht

Auch hier scheint das Muster sehr eindeutig, aber durch das Hinzufügen weiterer Merkmale verringert sich die Datengrundlage weiter.

So minimieren Sie den Zufall

Die Frage ist also: Wie lassen sich Muster zuverlässig identifizieren und Zufall ausschließen?

Eines vorweg: Der Einfluss des Zufalls lässt sich niemals komplett ausschließen. Selbst bei 200 Münzwürfen wäre es theoretisch möglich, dass jedes Mal Zahl erscheint – es ist lediglich sehr, sehr unwahrscheinlich. 

Aus diesem Grund muss die Frage anders gestellt werden: Wie wahrscheinlich ist es, dass die beobachtete Verteilung auf Zufall zurückgeht?

Bei der Beantwortung helfen sogenannte statistische Signifikanztests oder Hypothesentests. Hiermit kann ermittelt werden, ob eine vorher definierte Hypothese anhand der vorliegenden Daten verworfen werden kann – also die Abweichung groß genug ist, um statistisch signifikant zu sein. 

Die weitere Theorie kann an anderer Stelle nachgelesen werden – für die praktische Anwendung zur Optimierung der Gebote im Ads Konto wurde das folgende Excel-Sheet mit einem einseitigen Signifikanztest programmiert, welches auf Anfrage gern kostenfrei zur Verfügung gestellt wird und für jede Art von Wahrscheinlichkeit (Conversion-Rate, CTR, …) verwendet werden kann:

Abb. 4: Screenshot des Excel Sheets zur Signifikanztest der Stichproben

Die zugrunde liegenden Daten sind: 

Die Stichprobengröße n
Die Anzahl der Treffer x
Die Wahrscheinlichkeit p
Das Signifikanzniveau α

Angewendet auf das Beispiel der unterschiedlichen Conversion-Raten zwischen Männern und Frauen: Im betrachteten Zeitraum klickten 259 Männer die Anzeigen (-> die Stichprobengröße), wodurch 1,4 Conversions generiert wurden (-> die Anzahl der Treffer).

Das ergibt eine Conversion-Rate von 0,54%. Im Vergleich dazu betrug die kontoweite Conversion-Rate (-> die Grundwahrscheinlichkeit p) in diesem Zeitraum 0,88%.

Als nächstes muss festgelegt werden, mit welcher Wahrscheinlichkeit ein Irrtum ausgeschlossen werden soll – das sogenannte Signifikanzniveau. Hier sind beispielsweise 5% ein guter Startpunkt.

Werden diese Daten eingegeben, errechnet das Sheet eine Handlungsempfehlung: Ist die Abweichung signifikant, sollten die Gebote angepasst werden – andernfalls nicht.

In unserem Beispiel ist das Ergebnis deutlich: Die Gebote sollten nicht angepasst werden, da es sich mit hoher Wahrscheinlichkeit um Zufall handelt. Selbst bei einem deutlich höheren Signifikanzniveau von 30%, also einer sehr hohen Irrtumswahrscheinlichkeit, ist das Ergebnis immer noch nicht statistisch signifikant!

Wären mehr Daten vorhanden, also die Stichprobengröße sowie die Anzahl der Treffer beispielsweise um den Faktor 10 erhöht, sähe das Ergebnis wiederum deutlich anders aus.

An dieser Stelle werden sich viele Leser fragen, warum als Irrtumswahrscheinlichkeit nicht einfach 0% eingetragen wird. Die Antwort: Dieser Wert benennt nur die Wahrscheinlichkeit für einen Fehler erster Art, also das Ablehnen der Nullhypothese, obwohl Sie wahr ist.

In diesem Fall würden demnach die Gebote angepasst, obwohl es sich doch eigentlich um Zufall handelt.

Je kleiner das Signifikanzniveau gewählt wird, desto größer jedoch üblicherweise die Wahrscheinlichkeit für einen Fehler zweiter Art: Die Nullhypothese wird beibehalten, obwohl sie falsch ist. In diesem Fall würde das bedeuten, die Gebote werden nicht angepasst, obwohl die Conversion-Raten tatsächlich verschieden sind. Weitere Informationen dazu können hier nachgelesen werden.

Generell gilt: gibt es eine plausible Theorie, die eine unterschiedliche Conversion-Rate rechtfertigt, kann in der Praxis ein höheres Signifikanzniveau gewählt werden. Werden rein zufällige Daten verglichen, sollte ein Signifikanzniveau von maximal 5% genutzt werden, um ein belastbares Ergebnis zu erhalten.

Zu guter Letzt: je mehr Daten vorhanden sind, desto präzisere Aussagen liefert ein Signifikanztest – und desto geringer kann auch das Signifikanzniveau gewählt werden: Als Datenbasis sollte daher immer ein möglichst langer Zeitraum gewählt werden. 

Hierbei ist es aber natürlich wichtig, auf Saisonalitäten und andere Veränderungen beispielsweise im Sortiment oder in der Zielgruppe zu achten: Verändert sich die Conversion-Rate innerhalb der Stichprobe, nützt der schönste Signifikanztest nichts.

Haben Sie eine Frage, Anmerkung oder Interesse am kostenlosen Tool für Ihr Google Ads Konto? Schreiben Sie uns gern einen Kommentar oder kontaktieren Sie uns unverbindlich!